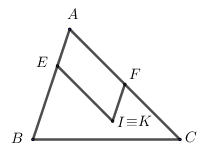
Cho tam giác ABC và đường tròn tâm O. Trên đoạn AB, lấy điểm E sao cho BE = 2AE,F là trung điểm của AC và I là đỉnh thứ tư của hình bình hành AEIF. Với mỗi điểm P trên ( O ) ta dựng điểm Q sao cho ( overrightarrow (PA) + 2 overrightarrow (PB) + 3 overrightarrow (PC) = 6 overrightarrow (IQ) ). Khi đó tập hợp điểm Q khi P thay đổi là:
Cho tam giác ABCABC và đường tròn tâm OO. Trên đoạn ABAB, lấy điểm EE sao cho BE=2AE,FBE=2AE,F là trung điểm của ACAC và II là đỉnh thứ tư của hình bình hành AEIFAEIF. Với mỗi điểm PP trên (O)(O) ta dựng điểm QQ sao cho →PA+2→PB+3→PC=6→IQ−−→PA+2−−→PB+3−−→PC=6−→IQ. Khi đó tập hợp điểm QQ khi PP thay đổi là:
Phương pháp giải
Gọi KK là điểm xác định bởi →KA+2→KB+3→KC=→0−−→KA+2−−→KB+3−−→KC=→0, chứng minh K≡IK≡I
Từ giả thiết ban đầu, sử dụng công thức 3 điểm, chứng minh II là trung điểm của PQPQ, suy ra quỹ tích điểm QQ khi PP di động.
Bài tập có liên quan
>> 2K8! chú ý! Mở đặt chỗ Lộ trình Sun 2026: Luyện thi chuyên sâu TN THPT, Đánh giá năng lực, Đánh giá tư duy tại Tuyensinh247.com (Xem ngay lộ trình). Ưu đãi -70% (chỉ trong tháng 3/2025) - Tặng miễn phí khoá học tổng ôn lớp 11, 2K8 xuất phát sớm, X2 cơ hội đỗ đại học. Học thử miễn phí ngay.
 |
 |
 |
 |
 |
 |
 |
 |