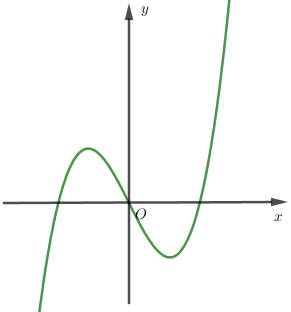
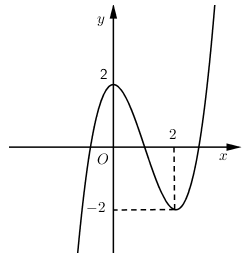
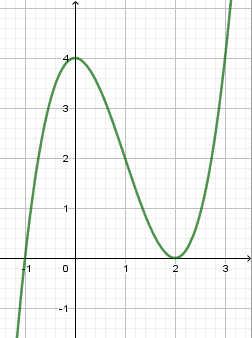
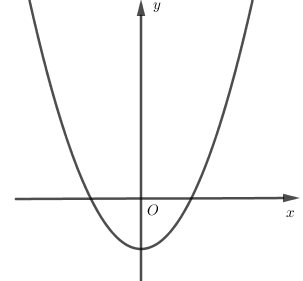
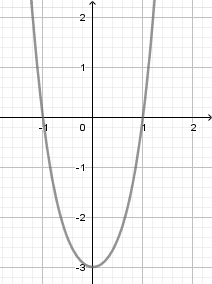
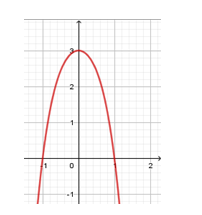
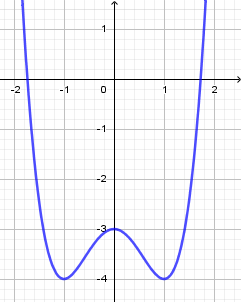
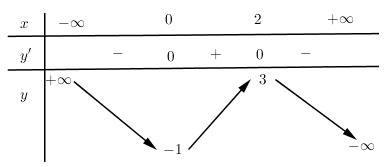
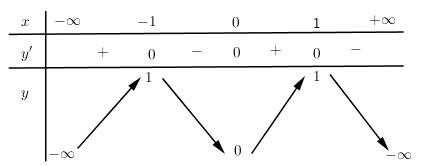
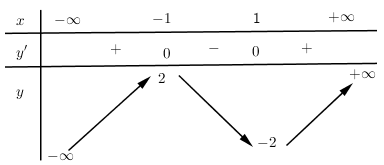
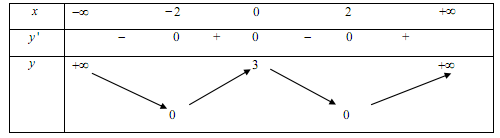
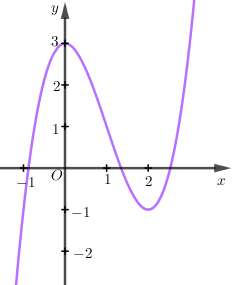
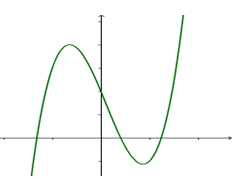
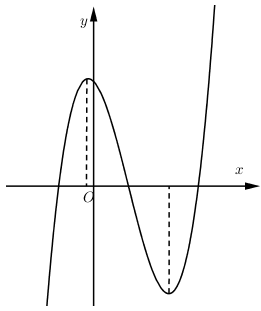
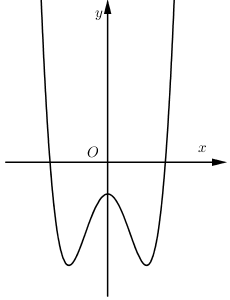
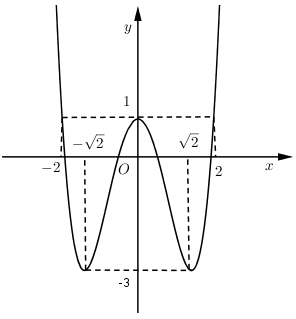
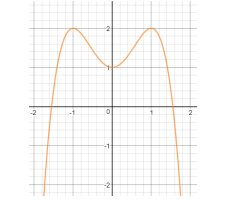
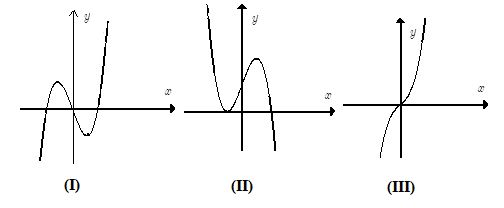
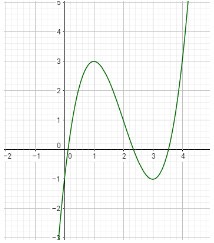
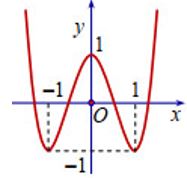
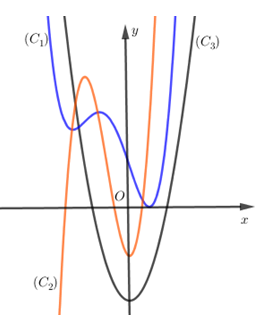
Cho hàm số (f( x ) = a(x^4) + b(x^3) + c(x^2) + + e, ) với (a,b,c,d,e thuộc mathbb(R). ) Hàm số (y = f'( x ) ) có đồ thị như hình vẽ. Trong các khẳng định sau, khẳng định nào đúng?
Câu 63276 Vận dụng cao
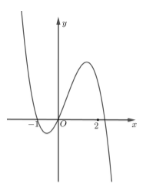
Cho hàm số f(x)=ax4+bx3+cx2+dx+e,f(x)=ax4+bx3+cx2+dx+e, với a,b,c,d,e∈R. Hàm số y=f′(x) có đồ thị như hình vẽ. Trong các khẳng định sau, khẳng định nào đúng?
Đáp án đúng: c
Phương pháp giải
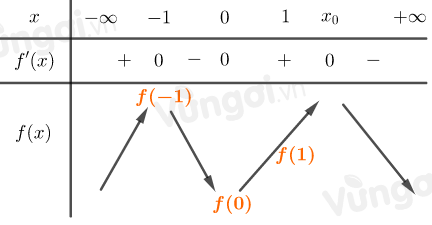
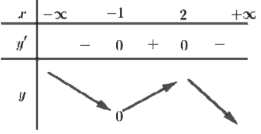
Từ đồ thị hàm số suy ra f′(0)=0;f′(x)>0,∀x∈(0;1)
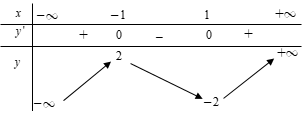
Lập bảng biến thiên của hàm số y=f(x)
Bài tập có liên quan
>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD - Click xem ngay) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |