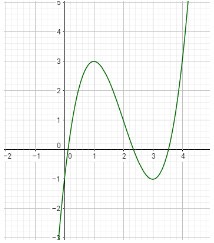
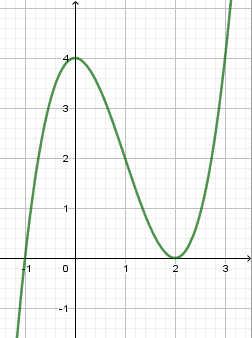
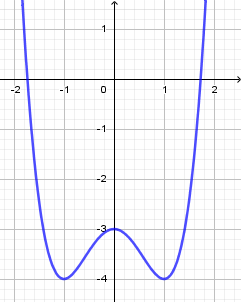
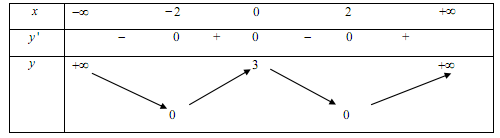
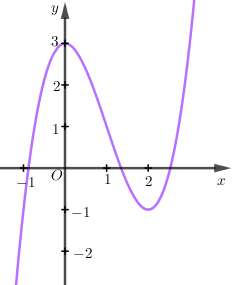
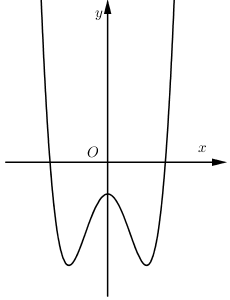
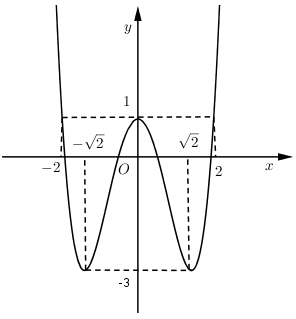
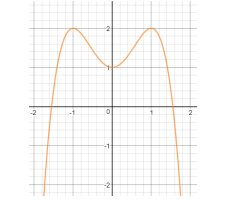
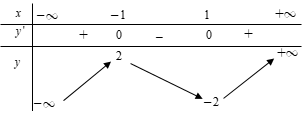
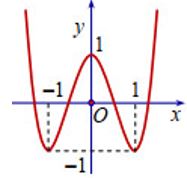
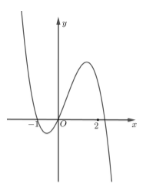
Cho đồ thị (C) của hàm số (y = (x^3) - 6(x^2) + 9x - 1 ) như hình vẽ. Hãy xác định số điểm cực trị của hàm số (y = (<=ft| x right|^3) - 6(x^2) + 9<=ft| x right| - 1 ).
Phương pháp giải
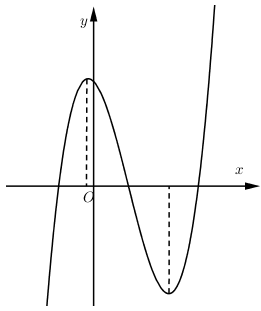
- Vẽ đồ thị hàm số y=f(|x|):
+ B1: Vẽ đồ thị hàm số y=f(x).
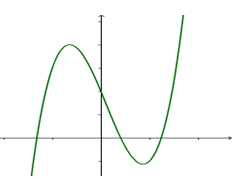
+ B2: Xóa đi phần đồ thị hàm số y=f(x) nằm phía bên trái trục Oy.
+ B3: Lấy đối xứng phần đồ thị hàm số y=f(x) nằm phía dưới bên phải trục Oy qua trục Oy.
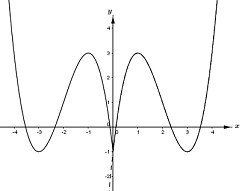
- Dựa vào đồ thị hàm số y=f(|x|) mới vẽ được xác định các điểm cực trị của hàm số (là điểm mà qua đó đồ thị hàm số đổi hướng từ đi lên thành đi xuống hoặc ngược lại).
Bài tập có liên quan
>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD - Click xem ngay) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |