I. Sơ đồ tư duy công thức quãng đường

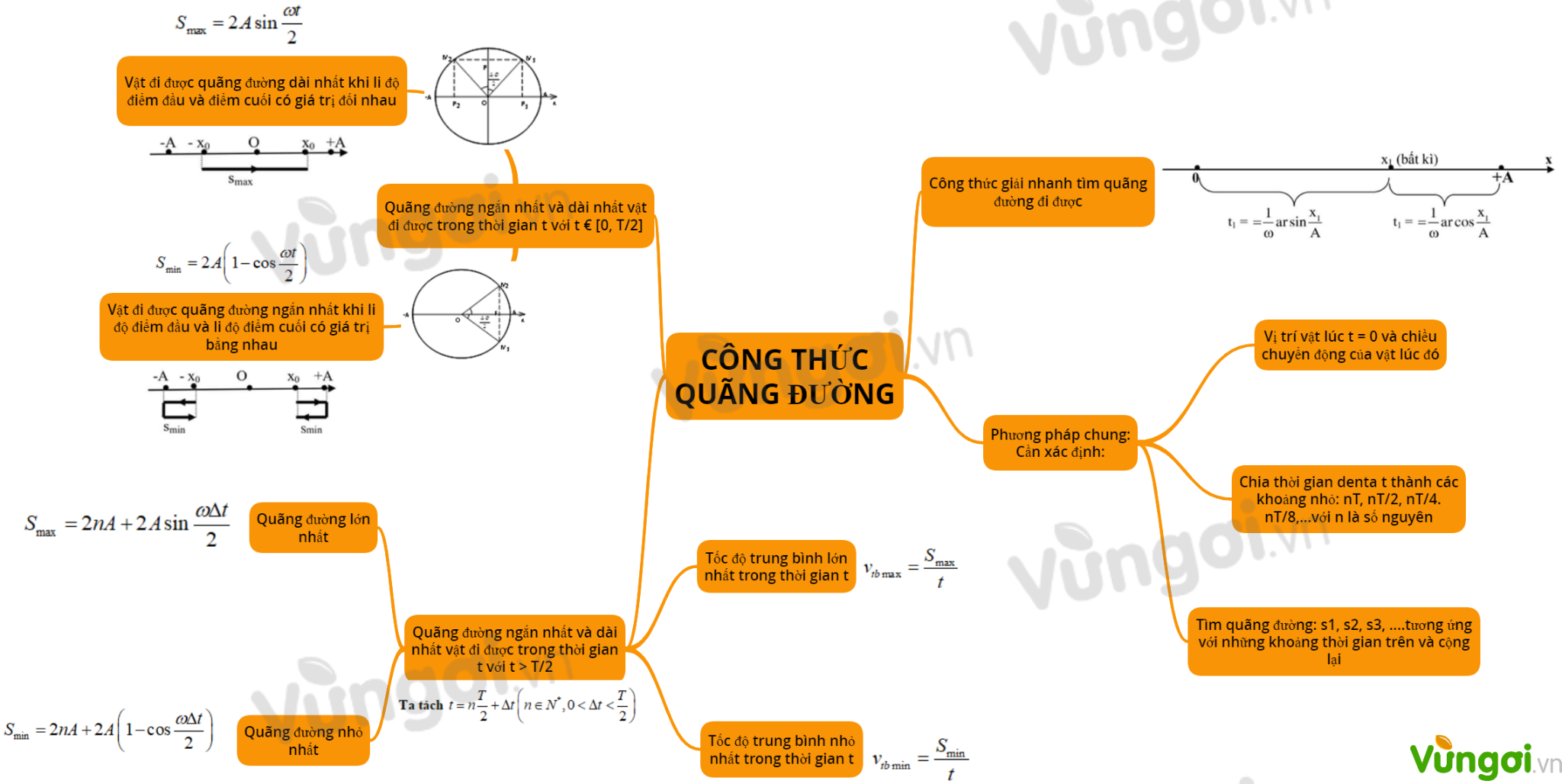
II. Ứng dụng vòng tròn lượng giác - Bài tập quãng đường - Tốc độ trung bình

I. DẠNG 1: QUÃNG ĐƯỜNG VẬT ĐI ĐƯỢC TỪ THỜI ĐIỂM T1 ĐẾN T2 - TỐC ĐỘ TRUNG BÌNH TRONG KHOẢNG THỜI GIAN ∆T

Chú ý:

+ Trong 1 chu kì, vật đi được quãng đường: $S = 4A$

+ Trong n chu kì, vật đi được quãng đường: $S = 4nA$

+ Trong $\dfrac{1}{2}$ chu kì, vật đi được quãng đường: $2A$

Phương pháp giải:

Tốc độ trung bình trong 1 chu kì: ${v_{tb}} = \dfrac{{4A}}{T} = \dfrac{{4A}}{{\dfrac{{2\pi }}{\omega }}} = \dfrac{{2A\omega }}{\pi } = \dfrac{{2{v_{{\rm{max}}}}}}{\pi }$

II. DẠNG 2: QUÃNG ĐƯỜNG LỚN NHẤT VÀ NHỎ NHẤT VẬT ĐI ĐƯỢC TRONG KHOẢNG THỜI GIAN ∆T - TỐC ĐỘ TRUNG BÌNH LỚN NHẤT VÀ NHỎ NHẤT TRONG KHOẢNG THỜI GIAN ∆T

Phương pháp giải:

Vật có vận tốc lớn nhất khi qua VTCB, nhỏ nhất khi qua vị trí biên nên trong cùng một khoảng thời gian quãng đường đi được càng lớn khi vật ở càng gần VTCB và càng nhỏ khi càng gần vị trí biên.

*  Trường hợp: 0 < Dt < T/2 

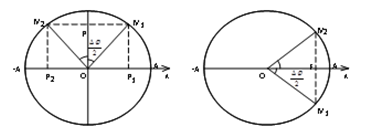
- Sử dụng mối liên hệ giữa dao động điều hoà và chuyển  đường tròn đều.

+ Góc quét: Dj = wDt.

+ Quãng đường lớn nhất khi vật đi từ M1 đến M2 đối xứng qua trục sin (hình 1)

+ Quãng đường nhỏ nhất khi vật đi từ M1 đến M2 đối xứng qua trục cos (hình 2)

* Trong trường hợp: Dt > T/2

Tách $\Delta t = n\dfrac{T}{2} + \Delta t'$  trong đó $n \in {N^*};0 < \Delta t' < \dfrac{T}{2}$

+ Trong thời gian $n\dfrac{T}{2}$ quãng đường  luôn là 2nA

+ Trong thời gian Dt’ thì quãng đường lớn nhất, nhỏ nhất tính như trên. 

+ Tốc độ trung bình lớn nhất và nhỏ nhất của trong khoảng thời gian Dt:

${v_{tbM{\rm{ax}}}} = \dfrac{{{S_{M{\rm{ax}}}}}}{{\Delta t}}$ và ${v_{tbMin}} = \dfrac{{{S_{Min}}}}{{\Delta t}}$ với SMax; SMin tính như trên.