Cho hình phẳng giới hạn bởi D = ( (y = tan x; , ,y = 0; , ,x = 0; , ,x = (pi )(3)) ). Thể tích vật tròn xoay khi D quay quanh trục Ox là V = pi ( (a - (pi )(b)) ), với a, , ,b thuộc R. Tính T = (a^2) + 2b.
Cho hình phẳng giới hạn bởi D={y=tanx;y=0;x=0;x=π3}.D={y=tanx;y=0;x=0;x=π3}. Thể tích vật tròn xoay khi DD quay quanh trục OxOx là V=π(a−πb),V=π(a−πb), với a,b∈R.a,b∈R. Tính T=a2+2b.T=a2+2b.
Phương pháp giải
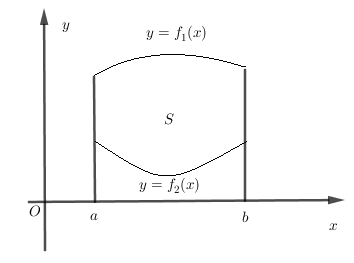
Thể tích khối tròn xoay khi xoay hình phẳng giới hạn bởi các đường y=f(x),x=a,x=by=f(x),x=a,x=b quanh trục Ox là: V=π.b∫af2(x)dx.V=π.b∫af2(x)dx.
Bài tập có liên quan
>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD - Click xem ngay) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |