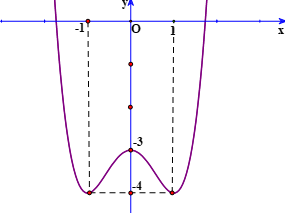
Tìm m để phương trình (x^5) + (x^3) - căn (1 - x) + m = 0 có nghiệm trên ( ( - vô cùng ;1) ].
Đáp án đúng: a
Phương pháp giải
- Nêu mối quan hệ giữa số nghiệm của phương trình và số giao điểm của d và (C).
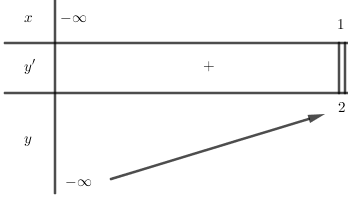
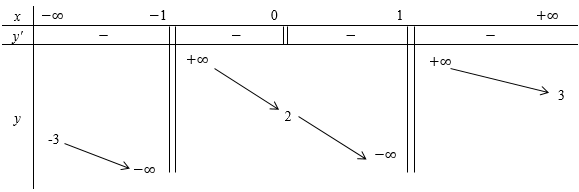
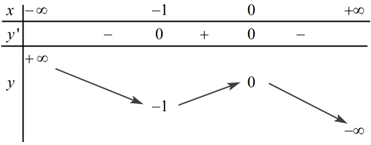
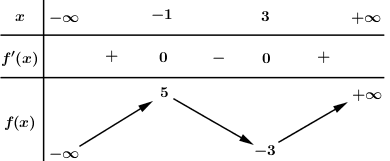
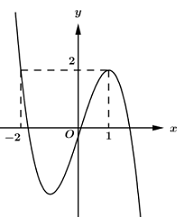
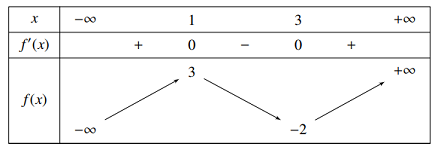
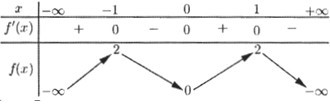
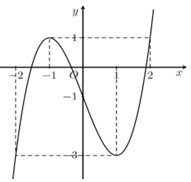
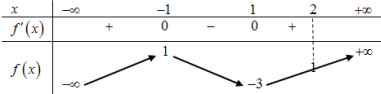
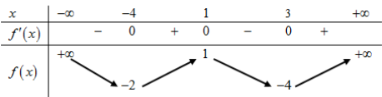
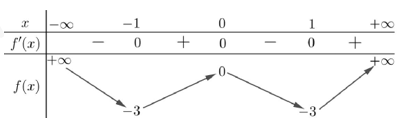
- Khảo sát hàm số y=x5+x3−√1−x trên (−∞;1] và từ đó suy ra điều kiện của m.
Bài tập có liên quan
>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD - Click xem ngay) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |